PERSONAJES MATEMÁTICOS
Pitágoras
Fue un filósofo y matemático griego considerado el primer
matemático puro. Contribuyó de manera
significativa en el avance de la matemática helénica, la geometría
y la aritmética, derivadas particularmente de las relaciones numéricas, y
aplicadas por ejemplo a la teoría de pesos y medidas, a la teoría de la música
o a la astronomía. Es el fundador de la Hermandad Pitagórica, una sociedad que,
si bien era de naturaleza predominantemente religiosa, se interesaba también en
medicina, cosmología, filosofía, ética y política, entre otras disciplinas. El
pitagorismo formuló principios que influyeron tanto en Platón como
en Aristóteles y, de
manera más general, en el posterior desarrollo de la matemática y en la filosofía racional en Occidente
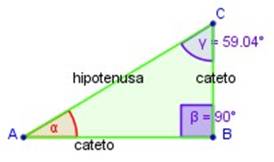
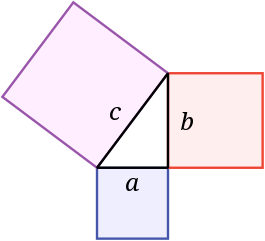
TEORÍA DE PITÁGORAS
El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa el
lado de mayor longitud del triángulo rectángulo es igual a la suma de los
cuadrados de los catetos los dos lados menores del triángulo, los que
conforman el ángulo recto.
Si un triángulo rectángulo tiene catetos de longitudes  y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se establece que:
, se establece que:
(1)
De la ecuación () se deducen fácilmente 3 corolarios de aplicación práctica:
 y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se establece que:
, se establece que:
(1)

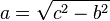 |  | 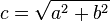 |
VIDEO
https://www.youtube.com/watch?v=I2nIgM_PDSE
Hiparco de Nicea
Fue un astrónomo, geógrafo y matemático griego. Entre sus aportaciones cabe
destacar: el primer catálogo de estrellas; la división del día en 24 horas de igual duración (hasta la invención
del reloj mecánico en el siglo XIV las divisiones del día variaban con las
estaciones); el descubrimiento de la precesión de los equinoccios; la
distinción entre año sidéreo y año trópico, mayor precisión en la medida de la
distancia Tierra-Luna y de la oblicuidad de la eclíptica, invención de la
trigonometría y de los conceptos de longitud y latitud geográficas.
Elaboración del
primer catálogo de estrellas que contenía la posición en coordenadas eclípticas de 1080 estrellas. Influyó en Hiparco
la aparición de una estrella nova,
Nova Scorpii en el año 134 a. C. y el pretender fijar la posición del equinoccio de primavera sobre el fondo de estrellas. Con el
propósito de elaborar dicho catálogo, Hiparco inventó instrumentos,
especialmente un teodolito,
para indicar posiciones y magnitudes, de forma que fuese fácil
descubrir sí las estrellas morían o nacían, si se movían o si
aumentaban o disminuían de brillo.
Además clasificó las estrellas según su intensidad, clasificándolas en magnitudes, según su grado de brillo.
APORTE
Hiparco
es el inventor de la trigonometría, para cuyo objeto consiste en relacionar las
medidas angulares con las lineales. Las necesidades de ese tipo de cálculos es
muy frecuente en astronomía.
Rheticus
fue un matemático, astrónomo, teólogo,cartógrafo, constructor de instrumentos musicales y médico austriaco.
APORTE
publicó las tablas de senos y cosenos
calculadas por él mismo. Otra contribución importante de Rheticus a las
ciencias fueron sus tablas de funciones trigonométricas realizadas con una
exactitud de 10 segundos, cuyo cálculo fue terminado por su discípulo
Valentinus Otho, quien las editó en 1596
OBRA
Y PENSAMIENTO
Rheticus
contribuyó considerablemente a la expansión del pensamiento
copernicano. Fue el único discípulo de Copérnico y lo pudo convencer
durante su estancia en Frauenburg de que publicara su obra maestra. Durante esa
época dio las primeras noticias sobre la obra copernicana, editada en su Narratio prima de libris revolutionum Copernici. De camino a Nuremberga para preparar la edición,
todavía publicó en Wittenberg la parte matemática, completada por las tablas de senos y cosenos calculadas por él mismo. La corrección de la galerada de De revolutionobus tuvo que dejársela a Andreas Osiander. Éste eliminó un tratado teológico sobre la
compatibilidad del sistema
heliocéntrico con la Biblia, sustiuyéndolo de forma anónima por un prefacio escrito por
él mismo, en el que presentaba el modelo como un simple modelo de cálculo. Más
tarde, Rheticus pubilicó Ephemeris ex fundamentis Copernici (Leipz.
1550).
TRIGONOMÉTRIA
La trigonométría es una rama de la matemática, cuyo
significado etimológico es la medición de los triángulos. En términos generales, la trigonometría es
el estudio de las razones trigonométricas: seno, coseno; tangente, cotangente; secante y cosecante. Interviene
directa o indirectamente en las demás ramas de la matemática y se aplica en
todos aquellos ámbitos donde se requieren medidas de precisión. La trigonométria se
aplica a otras ramas de la geometría, como es el caso del estudio de las esferas
en la geometría del espacio.
IDENTIDADES TRIGONOMETRICAS
Es una
igualdad entre expresiones que contienen funciones
trigonométricas y es válida para todos los valores del ángulo en los que
están definidas las funciones y las operaciones aritméticas involucradas.
COMO
EJEMPLO
Sabiendo que sen α = 3/5, y que 90º <α <180°. Calcular las restantes razones trigonométricas del ángulo α.


VIDEO
https://www.youtube.com/watch?v=Qc2amgLU0qk
LEY DE SENO
La ley de seno es una relación de tres igualdades que siempre se cumplen
entre los lados y ángulos de un triángulo cualquiera. En ocasiones
necesitarás resolver ejercicios que envuelven triángulos que no son
rectángulos. La ley del Seno y la del coseno son muy convenientes para
resolver problemas de triángulos en los que no hay ningún ángulo rectángulo
como los discutidos en la sección de trigonometría básica.
Veamos el
siguiente triángulo:
Podemos realizar el siguiente procedimiento:
En ΔAMC aplicamos el seno de A y obtenemos
y/b = sen A
despejamos para y,
obtenemos
------> y= b sen
A
En ΔBMC aplicamos el seno de B y obtenemos
y/a = sen B
despejamos para y,
obtenemos
------->
y= a sen B
Entonces:

La ley del seno nos dice que la razón entre la longitud de cada lado y
el seno del ángulo opuesto a el en todo triángulo es constante.
La ley del seno se escribirá como sigue:

VIDEO
https://www.youtube.com/watch?v=9m_jRVpgxqU
ley de coseno
La
ley de cosenos se puede considerar como una extención del teorema de pitágoras aplicable a todos los triángulos.
Ella enuncia así: el cuadrado de un lado de untriángulo es igual a la suma de
los cuadrados de los otros dos lados menos el doble producto de estos dos lados
multiplicado por el coseno del ángulo que forman. Si aplicamos este teorema al
triángulo de la figura 1 obtenemos tres ecuaciones:


Ejemplo:
Supongamos que en el triángulo de la figura 1
Solución:
Para calcular el valor del tercer lado, podemos emplear la ley de cosenos:
VIDEO
https://www.youtube.com/watch?v=Bp9TSlVDPIg
PREFUNTAS ICFES
A continuación se presentan ejemplos de preguntas de las categorías contextuales mencionadas. En las preguntas de selección se muestra la respuesta correcta. En las preguntas de respuesta construida-abierta, se presentan distintas maneras en que un estudiante puede responder, desde la perspectiva de validez de su respuesta en términos de la tarea solicitada.
El faro Pregunta 1
¿Cuánto dura el período de la secuencia de este faro?
A. 2 segundos.
B. 3 segundos. C. 5 segundos. D. 12 segundos.
Clasificación de la pregunta
Descripción: interpretar una gráfica de acuerdo con la información suministrada en un texto.
Proceso: interpretar. Contenido matemático: cambio y relaciones. Contexto: social.
Calificación de la respuesta
Respuesta correcta: C 5 segundos.
Pregunta 2
¿Durante cuántos segundos emite este faro destellos de luz a lo largo de 1 minuto?
A. 4
B. 12 C. 20 D. 24
Clasificación de la pregunta
Descripción: calcular una frecuencia en un intervalo de tiempo corto para adecuarla a un tiempo más prolongado.
Proceso: usar. Contenido matemático: cambio y relaciones. Contexto: social.
Calificación de la respuesta
Respuesta correcta: D-24.
Pregunta 3
En la cuadrícula de abajo traza el gráfico de una posible secuencia de destellos de luz de un faro que emita 30 segundos de destellos de luz cada minuto. El período de esta secuencia debe ser de 6 segundos.

Clasificación de la pregunta
Descripción: adecuar las condiciones de ocurrencia de un fenómeno variacional en un contexto dado, a una nueva situación.
Proceso: formular. Contenido matemático: cambio y relaciones. Contexto: social.
Calificación de la respuesta
Crédito total
Respuesta adecuada y pertinente el gráfico muestra una secuencia de luz y oscuridad con destellos de luz de 3 segundos por cada 6 segundos, y un período de 6 segundos. Esto se puede hacer de las siguientes maneras:
Crédito parcial
Respuesta adecuada pero no tan completa como la anterior: el gráfico muestra una secuencia de luz y oscuridad con destellos de luz de 3 segundos por cada 6 segundos, pero el período no es de 6 segundos. Si se presentan dos (2) períodos, la pauta debe ser la misma para ambos.
• 3 destellos de un segundo alternando con 3 períodos de oscuridad de un segundo. Construyendo bloques Pregunta 1
¿Cuántos cubos pequeños necesitará Susana para hacer el bloque que se muestra en el gráfico B?
... cubos.
Clasificación de la pregunta
Descripción: hallar la cantidad de cubos de un tamaño determinado para formar un bloque.
Proceso: interpretar. Contenido matemático: espacio y forma. Contexto: personal.
Calificación de la respuesta
Respuesta correcta: 12 cubos.
Pregunta 2
¿Cuántos cubos pequeños necesitará Susana para hacer el bloque macizo que se muestra en el gráfico C?
... cubos.
Clasificación de la pregunta
Descripción: hallar la cantidad de cubos de un tamaño determinado para formar un bloque.
Proceso: interpretar. Contenido matemático: espacio y forma. Contexto: personal.
Calificación de la respuesta
Respuesta correcta: 27 cubos.
Pregunta 3
Susana se da cuenta de que ha utilizado más cubos pequeños de los que realmente necesitaba para hacer un bloque como el que se muestra en el gráfico C. Se da cuenta de que podía haber construido un bloque como el del gráfico C pegando los cubos pequeños, pero dejándolo hueco por dentro.
¿Cuál es el mínimo número de cubos que necesita para hacer un bloque como el que se muestra en el gráfico C, pero hueco?
... cubos.
Clasificación de la pregunta
Descripción: analizar posibilidades de adecuación de la solución de un problema a una solución alternativa en una situación geométrica.
Proceso: formular. Contenido matemático: espacio y forma. Contexto: personal.
Calificación de la respuesta
Respuesta correcta: 26 cubos.
Tarifas postales
Pregunta 1
Juan quiere enviar a un amigo dos objetos que pesan 40 g y 80 g respectivamente. Según las tarifas postales de Zedlandia, decide si es más barato enviar los dos objetos en un único paquete o enviar los objetos en dos paquetes separados. Escribe tus cálculos para hallar el costo en los dos casos.
Clasificación de la pregunta
Descripción: comparar dos cantidades haciendo cálculos con base en una información suministrada de tarifas.
Proceso: usar. Contenido matemático: cantidad. Contexto: personal.
Calificación de la respuesta
Crédito total
Respuesta adecuada y pertinente implica mostar que es más barato enviar los objetos en dos paquetes separados. El costo será de 1,71 zeds para dos paquetes separados, y de 1,75 zeds para un único paquete que contenga los dos objetos.
Latidos del corazón
Pregunta 1
¿A partir de qué edad aumenta la máxima frecuencia cardiaca recomendada como resultado de introducir la nueva fórmula? Escribe tus cálculos.
Clasificación de la pregunta
Descripción: comparar variación de funciones usando expresiones algebraicas.
Proceso: interpretar Contenido matemático: cambio y relaciones. Contexto: científico.
Calificación de la respuesta
Crédito total
Respuesta adecuada y pertinente: Se acepta 41 ó 40.
220 – edad = 208 – 0,7 x edad resulta una edad = 40, por lo que las personas por encima de 40 años tendrán un máximo ritmo cardiaco recomendado más alto con la nueva fórmula. Pregunta 2
La fórmula para la máxima frecuencia cardiaca recomendada = 208 – (0,7 x edad) se usa también para determinar cuándo es más eficaz el ejercicio físico. Las investigaciones han demostrado que el ejercicio físico es más eficaz cuando los latidos cardíacos alcanzan el 80% de la máxima frecuencia cardiaca recomendada.
Escribe una fórmula que calcule la frecuencia cardiaca recomendada para que el ejercicio físico sea más efectivo, expresada en términos de edad.
Clasificación de la pregunta
Descripción: proponer una ecuación que se ajuste a unas condiciones establecidas.
Proceso: formular. Contenido matemático: cambio y relaciones. Contexto: científico.
Calificación de la respuesta
Crédito total
Respuesta adecuada y pertinente: Cualquier fórmula que sea el equivalente de multiplicar la fórmula del máximo ritmo cardiaco recomendado por el 80%.
Ejemplos de respuestas:
|